反彈开啓，轉債的“三段反射弧”框架

低價轉債也在漲，即使理論上它們對正股的敏感度並不高。這不僅與傳統理論不符，也與更早的經驗有一些差距。例如下圖爲金埔轉債，近期快速反彈，但畢竟平價只有60元附近，理論上屬於對正股不敏感的“偏債品種”。這個階段，轉債可能展現與經驗、傳統理論不符的“反射弧”。

圖表1：金埔轉債表現情況

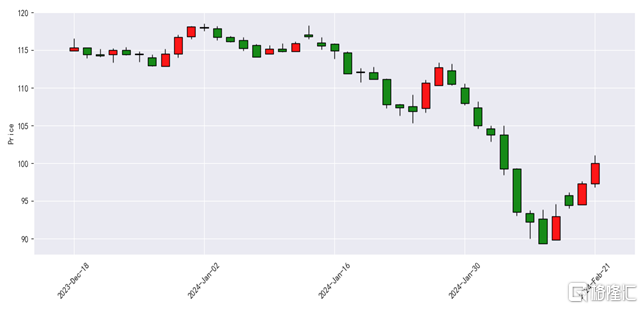
資料來源：Wind，中金公司研究部

臨時的彈性，以及負Gamma

低價券的“臨時彈性”實際不難解釋：畢竟此前跌出了退市風險的擔憂。更定量化地理解，所謂的“進可攻、退可守”，往往僅僅是轉債 vs 正股之間關系的一部分——通常所顯露出的那一部分——但曲线的左側，隨着正股下跌，退市風險加大，轉債重新“獲得了彈性”。特別是，轉債的極端風險不同於普通債券，它是與股價相關的：按照退市規則，當股價越接近1元、市值越接近3億元，其風險越大。實際上有：

圖表2：示意圖：當下低價券"彈性"的來源

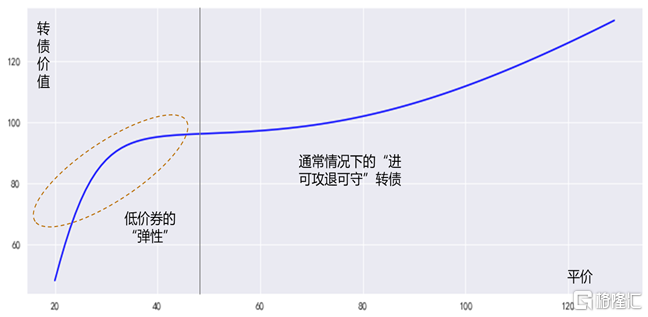
資料來源：Wind，中金公司研究部

這個現象存在兩個影響，對應轉債的兩個希臘字母，即delta與gamma：

1.Delta方面無需多言，股價上漲時公司與退市風險也漸行漸遠，可以用下面的公式表示一個轉債“不退市”的概率，即N(d3)。

圖表3：轉債不退市概率的模型

from scipy.stats import normimport numpy as npdef 不退市概率(S, K, vol_his, t): '''S爲平價，k爲退市條件觸發時轉債平價，即退市线，vol_his和t分別爲波動率和期限''' d3 = np.log(S/K) / vol_his / t ** 0.5 return norm.cdf(d3)

資料來源：中金公司研究部

而按照導數的公式，假設不考慮退市風險情況下、簡單用BS公式計算的轉債價值函數爲f，轉債的不退市概率函數爲g，有下面公式。可以簡單理解爲：後一項爲低價的轉債增加了彈性。

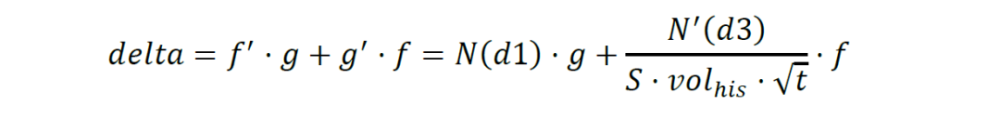
2. 但更重要的是，實際上有的品種要邁入“負Gamma”的階段了。顯然在引入退市風險的情況下，求Gamma的解析式會更爲冗長（更實用的是數值解，如下），但在上圖中已經顯示得很明確。

圖表4：轉債Delta和Gamma的計算

def bsCB(s, x, t, vol, rf): '''轉債專用,忽略了期間票息,X爲到期贖回價''' d1 = (np.log(s / x) + (rf + 0.5 * (vol ** 2)) * t) / (np.sqrt(t) * vol) d2 = d1 - vol * np.sqrt(t) return s * norm.cdf(d1) + x * np.exp(-r * t) * (1 - norm.cdf(d2)) def delta(s, x, t, vol, rf, k, vol_his): d1 = (np.log(s/x) + rf + 0.5 * t * vol ** 2) / (vol * t ** 0.5) d3 = np.log(s/k) / vol_his / t ** 0.5 price = bsCB(s, x, t, vol, rf) return norm.cdf(d1) * 不退市概率(S, K, vol_his, t) + \ norm.pdf(d3) * price / (s * vol * t ** 0.5) def gamma(s, x, t, vol, rf, k, vol_his): '''gamma直接用差分做，但請注意此處考慮擇券使用，s的間隔取一倍標准差，稍大''' ret = delta(s * np.exp(vol_his), x, t, vol, rf, k, vol_his) - \ delta(s * np.exp(-vol_his), x, t, vol, rf, k, vol_his) ret /= s * (np.exp(vol_his) - np.exp(-vol_his)) return ret

資料來源：中金公司研究部

就擇券來講，通常我們認爲Gamma要比Delta更爲重要——因爲Delta的發揮依賴於股價的方向，而Gamma有波動就可以了。而對於不必非常定量的投資者而言，需要進行的是一個更務實的選擇：對於低價轉債，剔除高違約風險券後（方法可見《退市風險模型與策略的Python實踐》），如果溢價率仍高且下修可能性不大，那么大概率其delta已經進入越漲越削弱的階段了——以當下低價券的數量之龐大，我們沒有必要在這樣的個券上停留太久。

下表是當下轉債中平價較低的一些品種，可以看到，考慮上述因素後，有的品種delta明顯要高於單純B-S公式計算的數值甚至超過1，但也可能存在負Gamma的情況。

圖表5：部分債性品種的Delta與Gamma（2月19日數據）

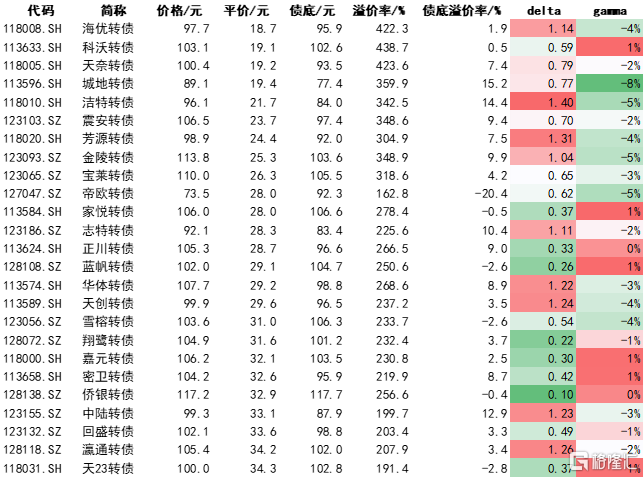
資料來源：Wind，中金公司研究部

傾斜的波動率曲线，平衡段的紅利區

轉債“反射弧”的異常還出現在“平價 vs 隱含波動率”曲线上。在轉債市場，波動率的傾斜由來已久，近期隨着風險偏好下滑，這種現象表現得非常“標准”——平價越高、隱含波動率（即估值）越低，下圖爲當前的情況。這當然與市場仍不高漲的預期，以及更關鍵的條款博弈情況有關。但關鍵是，這將如何影響當下轉債的投資性質。

圖表6：波動率的傾斜：截至2月19日數據

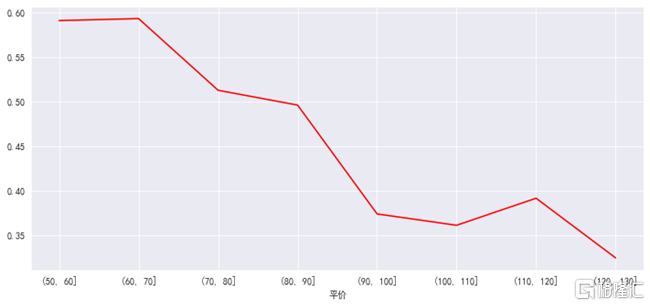
資料來源：Wind，中金公司研究部

至少，以下幾點投資者應有所認識：

1、當下，存在一個統計上的"紅利區"：當平價在90~105元附近時，平均隱含波動率下降不快，且在平價下跌時其隱含波動率能夠得到提升。簡單理解，若正股上漲，這些品種距離贖回還遠，若下跌，市場开始期待下修保護。

2、但對不同平價的轉債而言，其意義不同：平衡性品種對隱含波動率的敏感度更高，而偏股、偏債則較低。數字上可以抽象爲：“vega / close”，如下圖。結合當下市場狀態，會出現對股性、平衡性品種更有利，債性品種相對弱化的性質：對於股性轉債來說，股價上漲伴隨估值（隱含波動率）壓縮，但此時轉債對估值敏感度下降。而股價下跌伴隨估值提升，此時轉債對估值的敏感度也在提升，相當於附加了更多保護性。但對於平價80元以下的債性品種，情況則可能相反。自然這會影響轉債的性價比，而優勢與劣勢的分界點大約在平價90元附近。

圖表7：不同平價品種的vega值

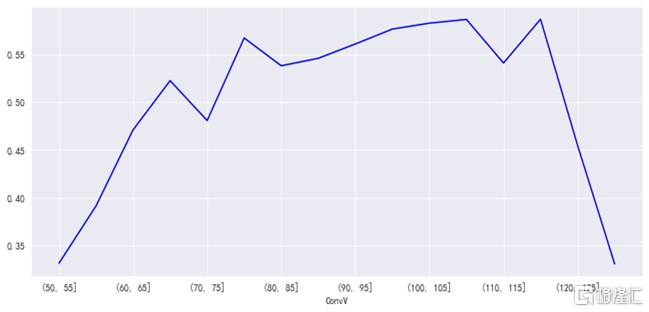
資料來源：Wind，中金公司研究部

3、股性券估值低是否是機會？是，但不多——當下平價120元~130元的品種數量僅剩5個。雖然歷史上股性轉債的隱含波動率也低於其他品種（考慮條款），但前期調整顯然更爲激烈。綜合來看，這些品種不僅具備了進攻性，也具備一定的凸性。

圖表8：部分平衡性、股性品種（斜體爲可能達到贖回條件的）

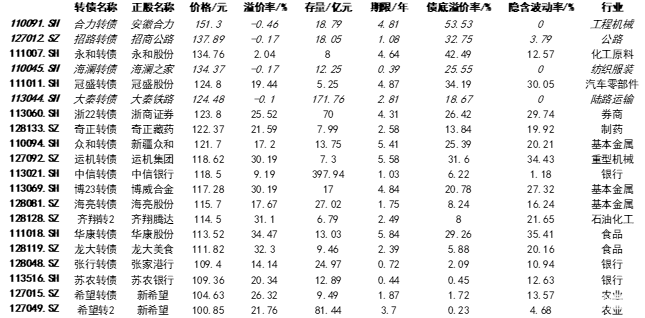
資料來源：Wind，中金公司研究部；注：數據截至2023年2月19日

小結

1、債性券的“彈性”與負Gamma：對於一些股價上漲即可遠離退市擔憂的券，此前及當下階段表現出一些彈性是合理的現象，但隨着風險化解，退市風險走遠，此後可能也要迎來負Gamma的問題——而隱含波動率的傾斜也對這些品種的削弱；

2、顯然市場上債性券數量最多，此前我們也建議投資者在此處布局，但當下到了可以更“挑剔”的時候。我們建議對低價券：

1）對動量做篩選，這是固定搭配，當下的意義在於高動量的品種有更大的可能性向平衡性乃至股性過渡；

2）對溢價率已經超過50%的品種，考慮下修的可能性，我們在此前的報告中給出過下修的一些規律，而近期下修的數量也達到了歷史頂峰。至少對於溢價率高、下修可能性很低的品種而言，投入太多自然會降低持倉效率。

圖表9：部分債性品種指標

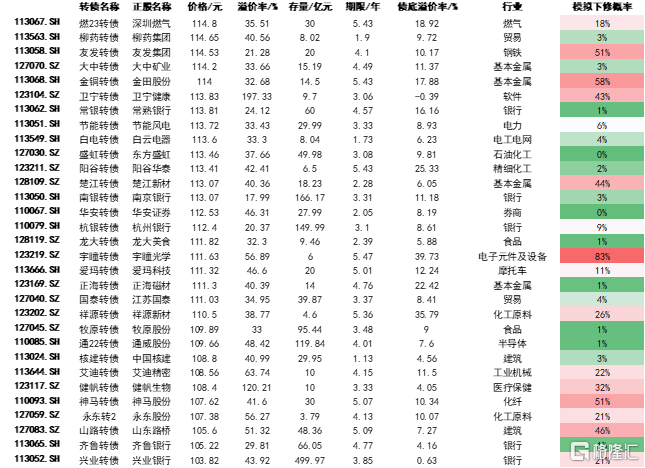
資料來源：Wind，中金公司研究部；注：數據截至2024年2月19日

3、策略配置上投資者可能要逐步向平衡性、股性過渡，當下可能更主要受限於數量。

4、我們暫無必要討論連續反彈中是否過熱，屆時市場會給出信號。

注：本文摘自中金公司2024年2月23日已經發布的《反彈开啓，轉債的"三段反射弧"框架》；楊冰分析員 SAC 執業證書編號：S0080515120002 SFC CE Ref：BOM868、羅凡分析員 SAC執業證書編號：S0080522070003 SFC CE Ref：BUL744、陳健恆分析員 SAC 執業證書編號：S0080511030011 SFC CE Ref：BBM220