關於十年美債利率的定價方程和數學的意義

引子

近期，美債的期限利差見頂回落，已經回落至-43bp附近。

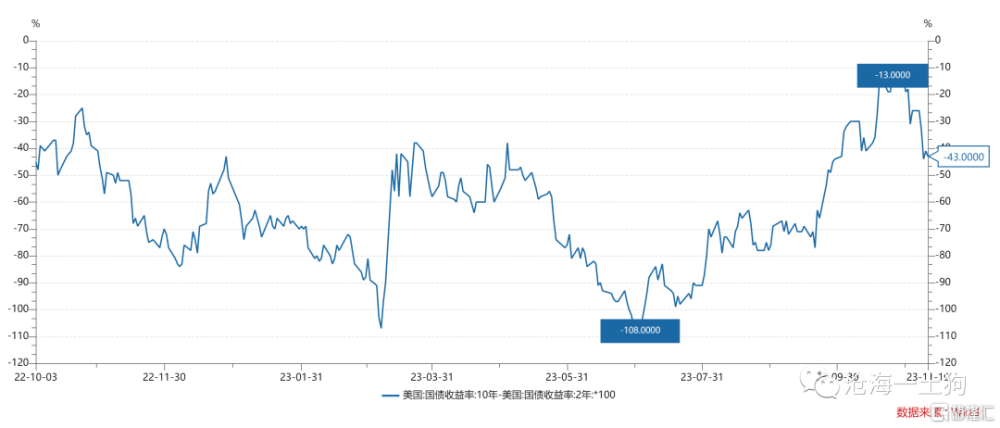
不少投資者會有這樣的疑問：

1、爲什么加息周期末期期限利差始終爲負？

2、這個階段期限利差的波動機制又是什么？

這篇文章將回答這兩個問題，並把我們之前的理論做一個整合。

兩年美債利率的定價方程

兩年美債利率是預期引導型貨幣體系的基石，我們從它的定價方程开始我們的討論。

在《預期引導型貨幣體系和美聯儲的預期管理框架》一文中，我們討論了兩年美債利率的實質：對聯邦基金利率預期路徑的一種測度。

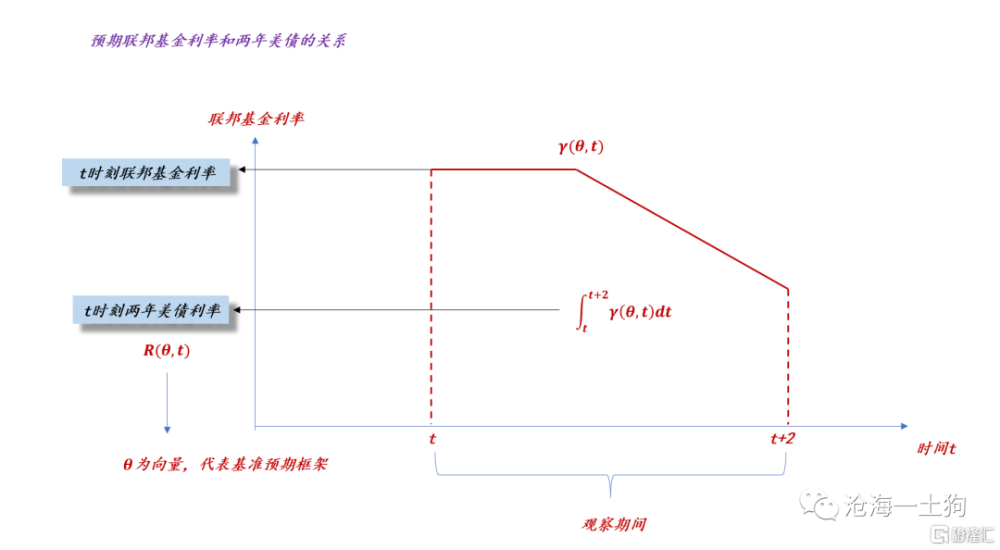
如上圖所示，對於這個測度，更加數學化的表達過程如下所示：

1、在t時刻，有對未來聯邦基金利率的預期函數γ（θ，t）；

2、我們對這個函數在【t,t+2】區間上積分，就可以得到兩年美債利率的函數；

3、其中，θ爲一組向量，代表基准預期框架。

我們用函數R（θ，t）代表γ（θ，t）在【t,t+2】區間上的積分，即我們經常所說的內部面積。

時間效應

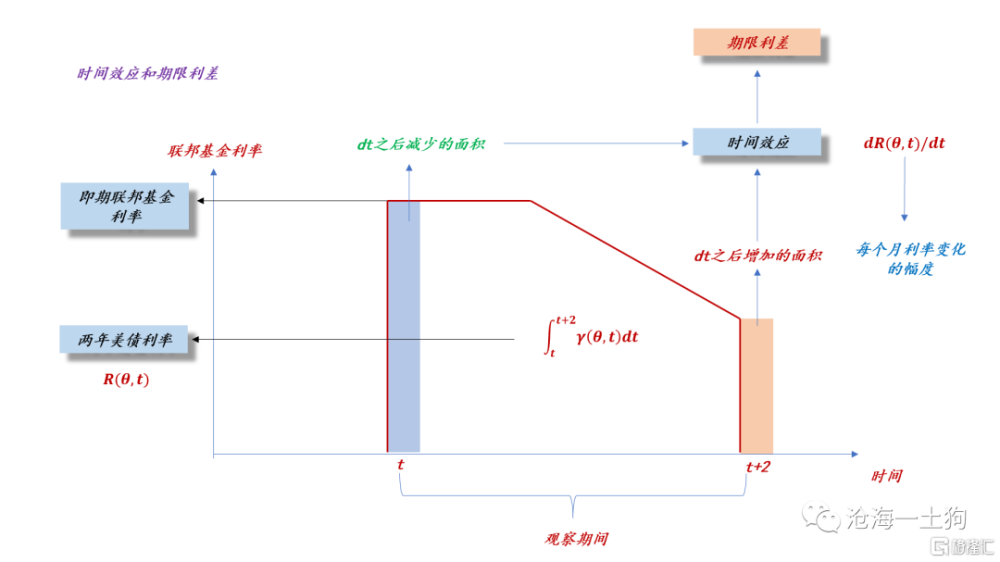
在《價格預測的本質》一文中我們有提到時間效應，在這裏我們將更詳細地論述它。

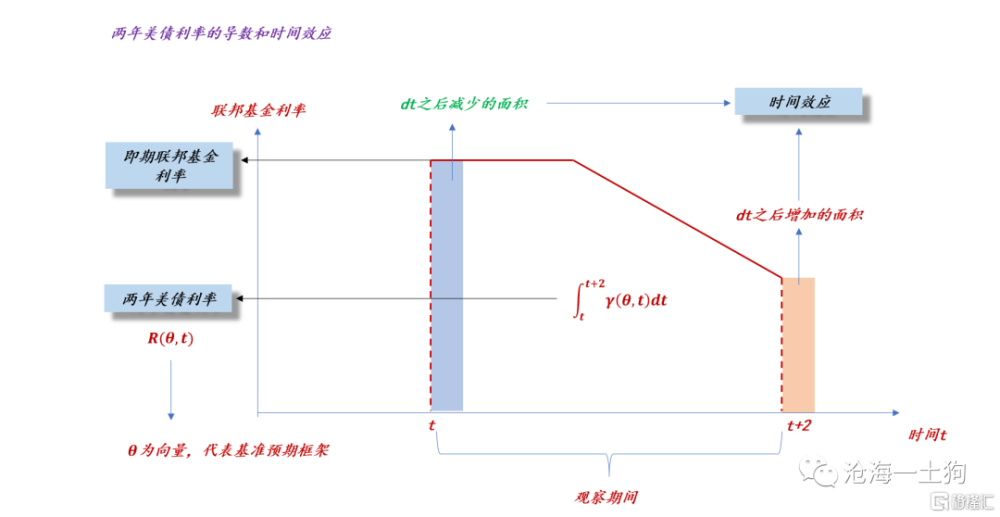
如上圖所示，我們讓時間往後推移一個單位，前端的面積減少了一塊，後端的面積增加了一塊，把一增一減綜合在一塊，就是時間效應。

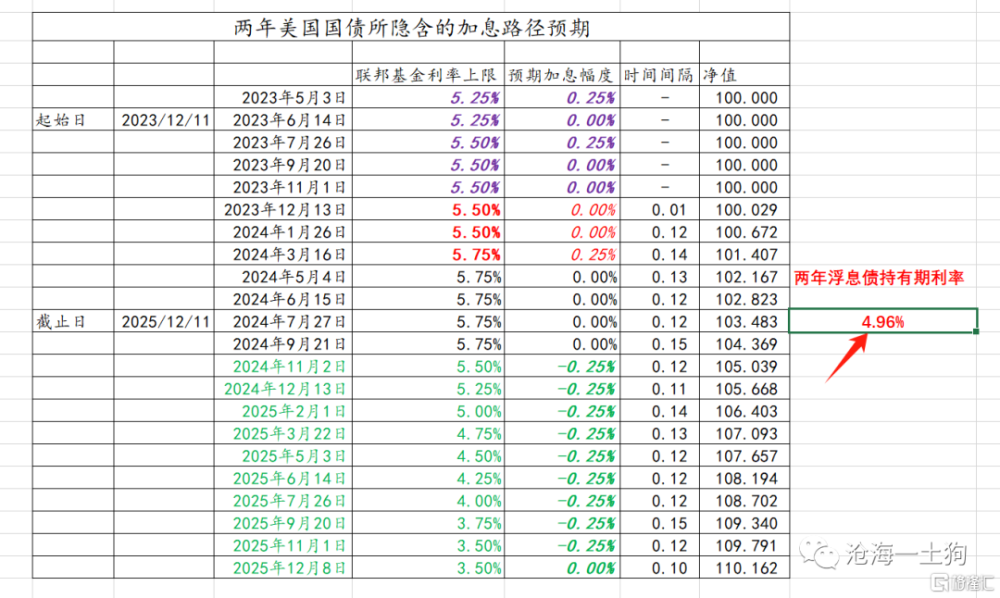
更進一步，我們可以結合實際情況去討論時間效應。假設θ不變，即基准預期框架保持：1、未來有一次加息；2、明年有兩次降息。

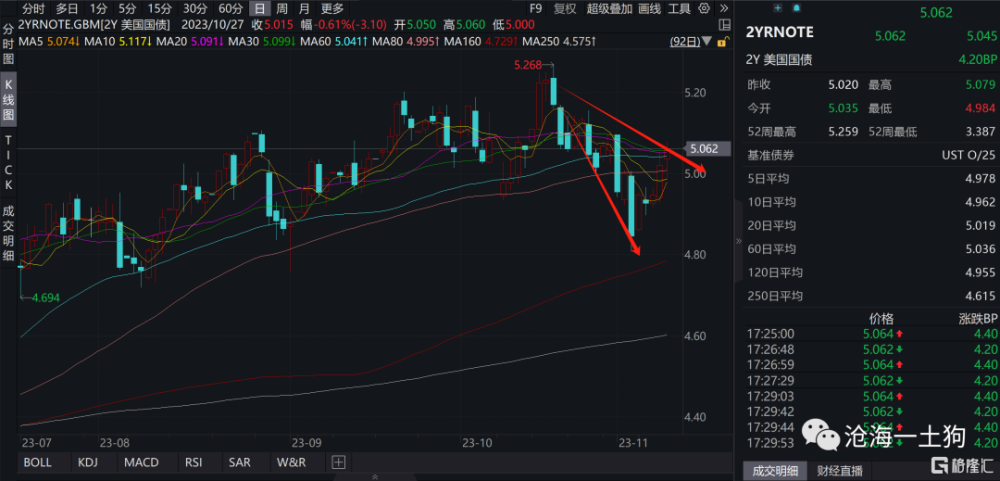
如下圖所示，11月11日所對應的兩年美債利率在5.06%。

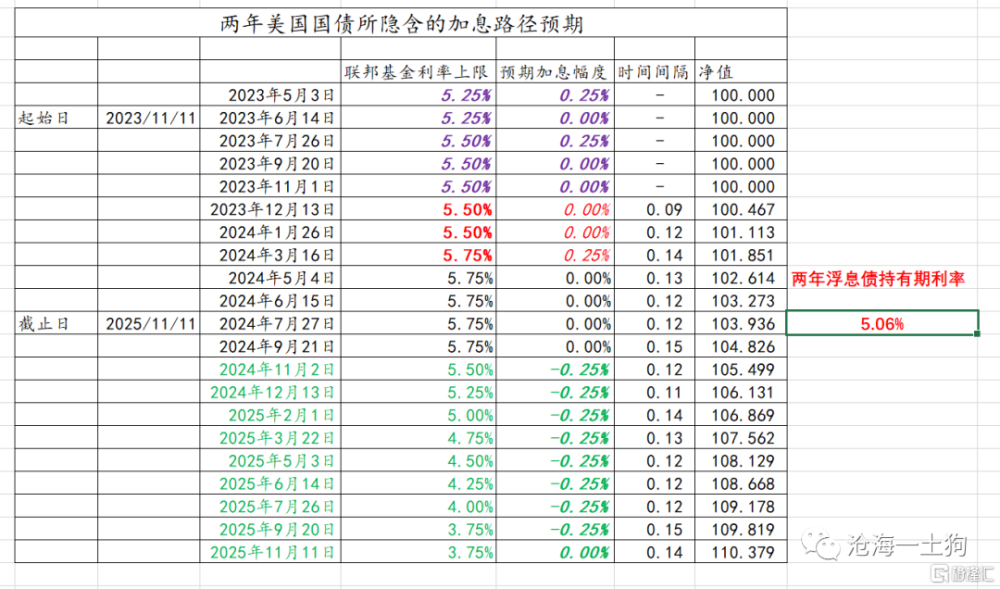
12月11日，所對應的兩年美債利率在4.96%。二者的差值就是-10bp，即時間效應。

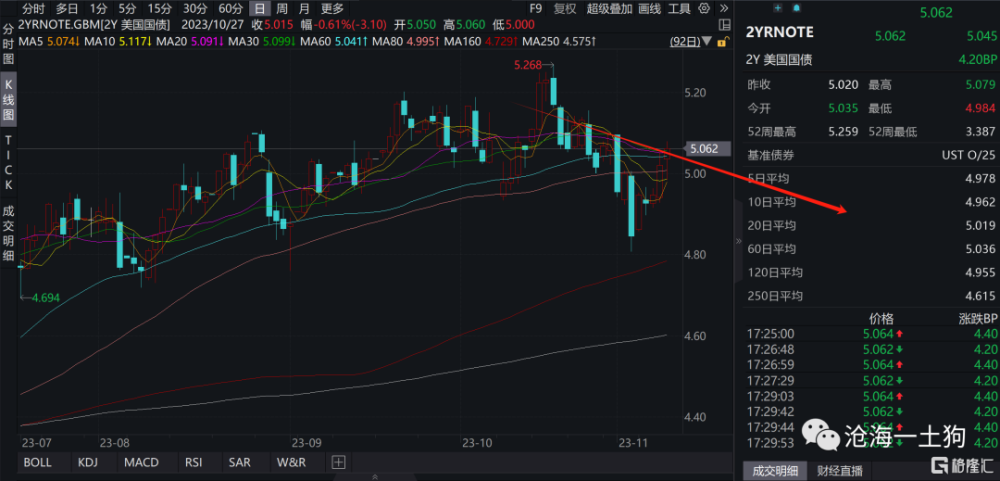
放到兩年美債利率的K线圖上，其實際含義更加明確：給定θ不變的情況下，預期一個月後兩年美債利率變化多少。

期限利差的定價方程

在數學上，我們可以把時間效應表達得更加精確，即R（θ，t）的導數，我們可以用dR（θ，t）/dt來表達。

不難發現，時間效應意味着市場對貨幣政策的預期，然而，還有其他影響期限利差的因素，最重要的是以下兩個：

1、對經濟的預期——風險偏好；

2、經濟現實狀況——貨幣的派生情況；

我們讓這兩個參數融合在μ和c兩個參數之中，於是，期限利差可以表示爲：

μ*dR（θ，t）/dt+c

於是，我們就得到了十年美債利率的定價方程：

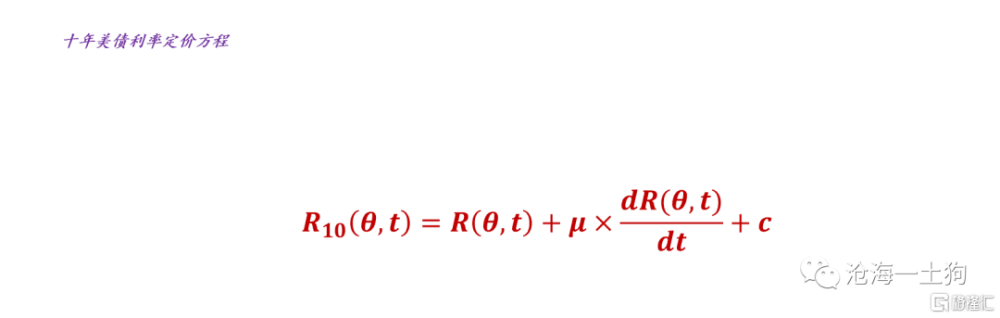
結束語

綜上所述，我們可以得到以下結論：

1、十年美債利率幾乎都是預期項，現實項有兩個：a、即期聯邦基金利率；b、經濟現實——貨幣的派生狀況；

2、美聯儲對十年美債利率的掌控力很強，因爲，他既掌控了兩年美債利率本身，也掌控了兩年美債利率的一階項；

3、經濟預期和經濟現實是美聯儲無法直接掌握的項，它們相對獨立；

4、在加息周期的末期，兩年美債利率的一階項必然爲負，因此，期限利差往往是負的，一階項的斜率越陡峭，期限利差負值的程度越深；

5、在加息周期的末期，美聯儲重點管控的不是兩年美債利率本身，而是，兩年美債利率的一階項：

6、數學的意義不僅僅在於計算具體的數字，而在於具備一致性地去表達復雜的客體關系，其背後的要點是兩個：a、定義良好；b、一致性體系；

7、不要老去想現實，要利用數學語言，沿着預期這條道往下走，現實的確重要，但跟預期比起來，它的權重實在是太小了；

ps：數據來自wind，圖片來自網絡

標題：關於十年美債利率的定價方程和數學的意義

地址：https://www.iknowplus.com/post/50751.html